Penyimpangan kuartil adalah bagian dari matematika dan statistik. Ada dua jenis deviasi, yaitu standar deviasi dan kuartil. Kali ini kita akan membahas lebih dalam mengenai kuartil simpangan yang banyak digunakan dalam pengolahan data.
Statistik biasanya digunakan untuk mengumpulkan dan juga mengolah data baik berupa data tunggal maupun kelompok. Ukuran dan skala data juga dapat dihitung dalam skala besar dan kecil. Ilmu statistika nantinya akan dibedakan dalam beberapa sub bab.
Mengetahui Kuartil

Sebelum masuk ke dalam pengertian simpangan, Anda harus mengetahui terlebih dahulu bahwa statistik dibagi menjadi beberapa bagian dalam hubungannya dengan ukuran dan letak data. Pembagian ini meliputi kuartil, persentil, dan desil.
Ketiganya memiliki perbedaan yang sangat mencolok. Namun, mari kita bicara lebih banyak tentang kuartil deviasi. Kuartil adalah angka yang membagi data berurutan menjadi 4 bagian yang sama atau sama dalam jumlah dan jangkauan. Jika Anda memiliki 16 buah data maka tepat untuk membagi data menjadi 4.
Namun, jika Anda memiliki data yang ganjil dan tidak dapat dibagi dengan 4, kuartil juga dapat ditentukan menggunakan rumus simpangan. Ada 3 nilai kuartil utama yaitu kuartil bawah (Q1), kuartil tengah (Q2), dan juga kuartil atas (Q3).
Memahami Penyimpangan Kuartil
Kuartil adalah ukuran dan penempatan kumpulan data. Sedangkan tabungan adalah ukuran penyebaran data. Atau dapat juga didefinisikan sebagai jarak antar kuartil yang merupakan setengah dari jarak antar kuartil. Juga dikenal sebagai rentang semi-kuartil atau simpangan antar-kuartil.
Kuartil deviasi adalah selisih antara kuartil atas dan kuartil bawah. Pertama-tama Anda harus bisa menentukan nilai atas, kemudian menentukan juga nilai kuartil bawah. Nilai simpangan kuartil ini dapat digunakan untuk melihat range dari berbagai kuartil.
Misalnya melihat dari kuartil ke-2 ke kuartil ke-1, kuartil ke-3 ke kuartil ke-2, dan seterusnya. Nilai penyimpangan kuartil ini sebenarnya adalah jarak rata-rata kuartil dalam data. Dalam rumusnya, simpangan kuartil dapat ditulis sebagai berikut:
Qd = ½ (Q3-Q1)
Informasi:
Qd = kuartil deviasi
Q3 = kuartil ke-3 atau atas
Q1 = kuartil pertama atau lebih rendah
Mungkin sebagian dari Anda masih bingung bagaimana cara menentukan kuartil. Ada berbagai cara untuk data tunggal dan data grup. Anda bisa berlatih sebelum menghitung simpangan kuartil.
Jenis Penyimpangan Kuartil

Secara umum, jenis kuartil deviasi dapat dibagi menjadi kuartil bawah, tengah, dan atas. Ini telah disebutkan sebelumnya, tetapi mari kita lihat lebih dekat untuk dapat menemukan perbedaannya.
1. Kuartil Bawah (Q1)
Awalnya yang harus Anda lakukan adalah menemukan nilai kuartil bawah. Caranya adalah dengan mengambil batas bawah dari nilai kuartil (Bb). Selanjutnya menentukan frekuensi kumulatif (fQ1) yang diperoleh dari jumlah frekuensi tepat di atas data frekuensi tersebut.
2. Kuartil Tengah (Q2)
Cara awal untuk mencari nilai kuartil tengah adalah dengan menentukan batas bawah nilai kuartil (Bb) dan frekuensi kumulatif dari banyaknya frekuensi di atas data. Selanjutnya, fQ2 adalah frekuensi dari data itu sendiri.
3. Kuartil Atas (Q3)
Awalnya yang harus Anda lakukan adalah menemukan nilai kuartil bawah. Caranya adalah dengan mengambil batas bawah dari nilai kuartil (Bb). Selanjutnya menentukan frekuensi kumulatif (fQ3) yang diperoleh dari jumlah frekuensi tepat di atas data frekuensi tersebut.
Untuk menentukan data kuartil, pertama-tama Anda harus mengurutkan data dari yang terkecil ke yang terbesar. Untuk menghitungnya juga harus diketahui apakah datanya ganjil atau genap. Cara menghitungnya adalah dengan menggunakan rumus berikut.
Data ganjil:
Q1 = 1/4 data (n+1)
Q2 = data ke 1/2 (n+1)
Q3 = data 3/4 (n+1)
Bahkan data:
Q1 = 1/4 data (n+2)
Q2 = ½ data ke 1/2 n + data ke (1/2 n + 1))
Q3 = 1/4 data (3n+2)
Jarak interkuartil
Penyimpangan kuartil, juga dikenal sebagai rentang semi-kuartil, adalah setengah dari rentang kuartil. Pengetikan ini dapat diartikan dalam rumus berikut Q3-Q1 atau disebut juga JAK = rentang antar kuartil.
● Rumus Rentang: J = Xmax – Xmin
● Rumus Jangkauan Kuartil Antar: H = Q3 – Q1
● Rumus Penyimpangan Kuartil: Qd = ½ (Q3-Q1)
● Rumus Langkah : L = 3/2H = 3/2(Q3-Q1)
● Rumus Pagar: Pagar dalam = Pd = Q1 – L; Pagar luar = Pl = Q3 – L
Cara Mencari Penyimpangan Kuartil

Menemukan simpangan kuartil sebenarnya sangat sederhana tergantung pada data yang Anda miliki. Ada dua jenis data, yaitu data tunggal dan data kelompok. Data tunggal biasanya hanya berisi satu jenis data.
Sedangkan data grup biasanya berisi range data atau data yang berada dalam range grup tertentu. Prinsip penentuan kuartil simpangan hampir sama, namun ada sedikit langkah tambahan pada data yang dikelompokkan.
Berikut cara mencari simpangan kuartil, yaitu:
1. Pelajari dan Sortir Data
Data harus diurutkan dalam skema dari yang terkecil hingga terbesar. Untuk itu diperlukan pengurutan data terlebih dahulu agar lebih mudah mencari nilai kuartil atas, bawah, dan tengah. Jika datanya berurutan, maka Anda bisa langsung mengerjakannya.
2. Bagilah data menjadi 3 bagian yang sama
Dalam data tunggal, mungkin cukup mudah membagi data dalam komposisi yang sama. Berbeda dengan data yang dikelompokkan, Anda harus mencarinya menggunakan rumus. Ini akan dijelaskan lebih rinci dalam contoh soal.
3. Temukan Jangkauan Antar Kuartil
Kisaran antara kuartil dapat ditemukan dengan mengurangkan kuartil atas (Q3) dan bawah (Q1). Selanjutnya, angka yang dihasilkan dari pengurangan tersebut merupakan rentang data antar kuartil. Untuk menemukannya sangat mudah.
4. Tentukan Penyimpangan Kuartil
Setelah mendapatkan jangkauan antarkuartil, simpangan antarkuartil akan mudah dicari, karena hanya perlu mengalikan data jangkauan antarkuartil dengan koefisien 0,5 atau ½ sesuai dengan rumus yang telah diberikan.
Contoh Soal 1
Diketahui kelompok data kandungan logam berat dalam air adalah 35, 50, 20, 45, 30, 25, 30, 40, 45, 30, dan 35. Dari data tersebut, cari data rentang antara kuartil dan penyimpangan mereka.
Menjawab:
Dikenal:
35, 50, 20, 45, 30, 25, 30, 40, 45, 30, dan 35
diminta:
Jarak interkuartil
Deviasi
Menjawab:
Hal pertama yang harus dilakukan adalah mengurutkan semua data menjadi susunan yang valid dari yang terkecil hingga yang terbesar. Jadi Anda akan mendapatkan yang berikut ini:
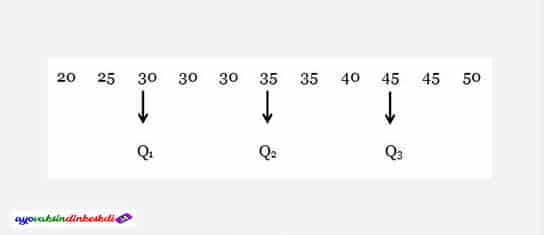
20, 25, 30, 30, 30, 35, 35, 40, 45, 45, 50
Selanjutnya adalah menentukan kuartil bawah, kuartil tengah, dan juga kuartil atas. Data ini merupakan data tunggal sehingga lebih mudah untuk membuat dan menentukan tiga kuartil.
Anda hanya perlu membaginya menjadi 3 bagian yang sama. Untuk itu diketahui bahwa:
Q1 = kuartil bawah = 30
Q2 = kuartil tengah = 35
Q3 = kuartil atas = 45
Dari analisis ini, jarak antar kuartil dapat dengan mudah ditentukan sebagai berikut:
H = Q3 – Q1
T = 45 – 30
H = 15
Di sebelah pencarian simpangan kuartil dapat menggunakan rumus:
Qd = ½ (Q3-Q1)
Qd = ½ (15)
Qd = 7.5, dimana nilai Q3-Q1 sudah didapat dari perhitungan range antar kuartil
Sehingga dapat disimpulkan bahwa jangkauan antar kuartil dari data tersebut adalah 15 dan kuartil simpangannya adalah 7,5.
Contoh Soal 2
Dalam data ini terdapat nilai ulangan matematika dalam satu kelas dengan jumlah siswa 40 orang. Nilai bervariasi dari 50-79. Tentukan nilai kuartil simpangan.
| Tanda | Frekuensi |
| 50-54 | 4 |
| 55-59 | 6 |
| 60-64 | 8 |
| 65-69 | 10 |
| 70-74 | 8 |
| 75-79 | 4 |
Menjawab:
Hal pertama yang harus dilakukan adalah menentukan frekuensi kumulatif untuk setiap data. Caranya adalah dengan menjumlahkan nilai frekuensi diatasnya dan yang dibawahnya. Maka dapat ditulis pada kolom sebelah kanan sebagai berikut
| Tanda | Frekuensi | Frekuensi kumulatif |
| 50-54 | 4 | 4 |
| 55-59 | 6 | 10 |
| 60-64 | 8 | 18 |
| 65-69 | 10 | 28 |
| 70-74 | 8 | 36 |
| 75-79 | 4 | 40 |
Dari data tersebut, cara mencari frekuensi kumulatif adalah dengan menjumlahkan 4 dan 6 menjadi 10. Kemudian menjumlahkan 10 dan 8 menjadi 18. Kemudian menjumlahkan 18 dan 10 menjadi 28.
Selanjutnya adalah mengetahui interval atau panjang kelas yaitu 5. Cara menghitungnya adalah dengan menghitung jumlah rentang bilangan. Misalnya di kisaran 50-54. Akan ada angka 50, 51, 52, 53, 54. Di kelas itu ada 5 angka.
Mencari simpangan kuartil, lalu apa yang harus dilakukan dalam menghitung kuartil bawah (Q1) dan juga kuartil atas (Q2). Anda dapat menghitung keduanya menggunakan rumus berikut.
Pertama temukan lokasi atau kelas kuartil. Di mana data adalah kuartil Q1 berada. Caranya adalah dengan:
¼ x 40 = 10 artinya, pada data yang mengandung frekuensi kumulatif 10 terdapat kelas kuartil bawah (Q1). ¼ adalah koefisien pengali. Sedangkan 40 adalah jumlah total frekuensi.
Tb = 55 – 0.5 = 54.5 dimana F= 4 dan f = 6Q1 = 54.5 + 5. ((10-4)/6)
Q1 = 54,5 + 5. (6/6)
Q1 = 54,5 + 5
Q1 = 59,5
Sehingga ditemukan bahwa kuartil bawahnya adalah 59,5
Selanjutnya adalah menentukan kuartil atas (Q3). Metodenya adalah sebagai berikut:
3/4 x 40 = 30 artinya, pada data yang mengandung frekuensi kumulatif 30 terdapat kelas kuartil atas (Q3). Oleh karena itu perlu diambil kelas yang memiliki frekuensi kumulatif lebih dari 30 yaitu kelas 70-74. ¾ adalah koefisien pengali. Sedangkan 40 adalah jumlah total frekuensi.
Tb = 70 – 0.5 = 69.5 dimana F= 28 dan f = 8
Q1 = 69,5 + 5. ((30 – 28)/8)
Q1 = 69,5 + 5. (2/8)
Q1 = 69,5 + 1,25
Q1 = 70,75
Qd = ½ (Q3 – Q1)
Qd = ½ (70,75 – 59,5)
Qd = 11,25 / 2
Qd = 5,625
Oleh karena itu ditemukan bahwa kuartil simpangan adalah 5,625
Itulah beberapa penjelasan tentang simpangan kuartil , pengertian, dan juga berbagai penjelasan penting lainnya. Memahami nilai simpangan akan memudahkan Anda dalam mengolah berbagai data kajian dan statistik yang nantinya akan sangat berguna.
Baca Juga Artikel Lainnya :
- Notasi Sigma Kelas 11 – Definisi, Rumus, dan Contoh Soal
- Bilangan dengan Pangkat Pecahan, Bentuk Akar, dan Contoh Soal
- Kuantitas Turunan Bersama Satuan, Dimensi, dan Contoh
- Fungsi caliper, cara pakai, contoh soal dll
- Pola Bilangan Segitiga, Fibonacci, Ganjil, Kotak, Dll (Lengkap)
- Ciri-Ciri Pangkat Beserta Pengertian, Sifat & Contoh Soal