Pola angka Matematika merupakan ilmu yang sering diterapkan dalam kehidupan sehari-hari. Misalnya dalam pembentukan formasi tari untuk pentas, hal ini tidak lepas dari penggunaan pola dalam angka.
Dalam pembahasan matematika, total ada 9 pola dalam bilangan yang harus dipelajari. Mulai dari pola ganjil, genap, segitiga, Fibonacci, hingga Pascal. Namun sebelum itu, simak dulu pengertian pola pada angka-angka di bawah ini agar lebih mudah dipahami.
Apa itu Pola Angka?
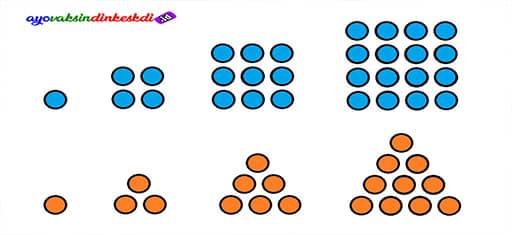
Pada penjelasan sebelumnya kamu sudah melihat salah satu contoh penerapan pola pada angka bukan? Tentunya sekarang setidaknya sudah ada gambaran tentang apa yang disebut pola dalam angka.
Jika dilihat dari asal katanya, pola berarti suatu bentuk atau susunan yang tetap. Sedangkan angka memiliki arti sebagai satuan besaran yang mengacu pada angka.
Jika dijumlahkan, maka pola angka adalah susunan angka atau urutan angka yang nantinya akan membentuk pola tertentu. Pola yang terbentuk dari susunan atau barisan tersebut kemudian akan menghasilkan rumus umum untuk menentukan suku ke-n suatu bilangan.
Artinya, setelah memahami pola bilangan yang berbaris, Anda bisa mendapatkan rumus untuk mengetahui hasil bilangan selanjutnya sesuai dengan pola tersebut. Rumus ini juga dapat digunakan untuk mencari bilangan kesekian yang disimbolkan sebagai suku ke-n yang sesuai dengan pola tersebut.
Seperti banyak pola yang ada di muka bumi ini, dalam operasi aritmatika matematika tidak hanya terdapat satu pola pada bilangan. Setelah dilakukan pengelompokan, terdapat 9 bentuk pola pada bilangan dengan rumus yang berbeda. Nantinya rumus ini akan diterapkan pada berbagai macam soal.
Bentuk dan Formula Pola Angka
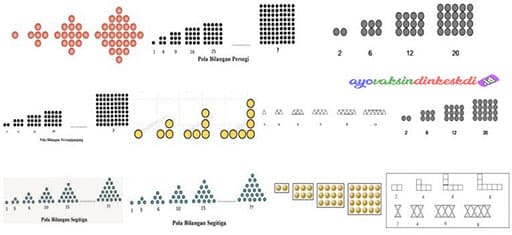
Berdasarkan penjelasan di atas, terlihat bahwa suatu bilangan yang disusun kemudian akan membentuk suatu pola tertentu. Susunan pola ini bisa bermacam-macam, mulai dari bilangan genap, ganjil, persegi, aritmatika, geometri, fibonacci, segitiga, dan Pascal.
Untuk mengetahui tujuan dari masing-masing bentuk pola tersebut, serta mengetahui rumus dan contohnya, simak penjelasannya di bawah ini:
1. Pola pada Angka Ganjil
Bentuk pertama yang akan dibahas kali ini adalah pola pada bilangan ganjil. Sesuai dengan namanya, pola ini tersusun dari angka ganjil. Sedangkan bilangan ganjil memiliki arti sebagai bilangan yang tidak habis dibagi 2.
Contoh angka tersebut adalah 1, 3, 5, 7, dan seterusnya. Dengan pola tersebut, akan diperoleh rumus pola bilangan ganjil sebagai berikut:
kamuN = 2n – 1
Informasi: N adalah bilangan asli yang merupakan barisan bilangan yang ingin dicari nilainya (thN)
Contoh: 1, 3, 5, 7, 9, …
Angka 1 adalah suku pertama (U1), angka 3 adalah suku kedua (U2), dst. Kemudian cari suku ketigaN, lalu cara menggunakan rumus diatas tadi. Misalnya suku ke-5 diketahui bernilai 9, mari kita buktikan dengan rumus di atas.
- kamuN = 2n – 1
- kamu5 = (2,5) – 1
- kamu5 = 10 – 1
- kamu5 = 9
Hasil perhitungan rumus sudah sesuai dengan data yang ada, artinya rumus diatas valid.
2. Pola pada Bilangan Genap
Jika poin pertama sudah membahas tentang bilangan ganjil, maka kali ini yang akan dibahas adalah pola susunan bilangan genap. Angka genap sendiri adalah angka yang akan habis jika dibagi 2. Contohnya 2, 4, 6, 8, dan seterusnya
Jika dihitung dengan teliti, contoh di atas akan habis jika dibagi dengan angka 2. Adapun rumus pola satu adalah sebagai berikut:
kamuN = 2n
Informasi: N adalah nomor urut N
Contoh: 2, 4, 6, 8, …
Dari barisan di atas, dapat disimpulkan bahwa setiap suku merupakan penjumlahan dari bilangan 2 suku sebelumnya. Sehingga suku ke-5 bernilai 10. Tapi bagaimana cara menghitungnya menggunakan rumus? Simak caranya di bawah ini!
Terbukti, hasil perhitungan manual menggunakan rumus menghasilkan angka yang sama.
3. Pola Bilangan Aritmatika
Bilangan urut aritmetika adalah bilangan yang susunan antara kedua sukunya mempunyai selisih tetap. Sehingga dalam aritmatika, banyaknya bilangan yang dijumlahkan antara satu suku dengan suku lainnya akan selalu sama.
Rumus pola pada bilangan aritmatika adalah:
kamuN = a + (n-1)b
Informasi:
- A adalah suku pertama dalam barisan tersebut
- B adalah perbedaan atau perbedaan antara satu suku dengan suku sebelumnya
- N adalah nomor urutN
Contoh: 4, 8, 12, 16, …
Dari barisan di atas jika dihitung secara manual maka dapat disimpulkan bahwa suku berikutnya merupakan penjumlahan suku sebelumnya dengan bilangan 4. Namun bagaimana jika yang ditanyakan adalah suku ke-22?
Tentu akan sangat merepotkan jika harus menghitung secara manual satu per satu. Untuk itu rumus pola pada bilangan aritmetika diatas semoga bermanfaat. Simak penyelesaian soal berikut ini!
- Diketahui: a = 4, b = 4
- Ditanya = U22?
- Dijawab =
- kamuN = a + (n-1)b
- kamu22 = 4 + (22-1)4
- kamu22 = 4 + 21,4
- kamu22 = 4 + 82
- kamu22 = 86
4. Pola pada Bilangan Geometri
Pola yang satu ini merupakan pola yang terbentuk dari susunan bilangan dengan perbandingan yang sama antara satu suku dengan suku sebelumnya. Apa rasio itu? Agar tidak bingung dan paham, simak contoh deret geometri berikut ini:
3, 9, 27, 81, 243, …
Dari contoh di atas, terlihat bahwa ada rasio yang sama antara kedua suku tersebut. Suku kedua diperoleh dari 3 x 3, suku ketiga diperoleh dari 9 x 3, suku keempat diperoleh dari 27 x 3, dan seterusnya. Angka 3 inilah yang disebut sebagai rasio.
Karena terkadang melibatkan angka besar yang akan sulit dihitung secara manual, maka dibentuklah rumus pola dalam geometri berikut:
kamuN = arn-1
Informasi:
- A adalah suku pertama (U1) di telepon
- R adalah rasio
- N adalah sukuN
Sedangkan untuk mencari rasio, Anda bisa menggunakan rumus ini:
r = UN/un-1
Atau jika rumusnya diterjemahkan, cara mencari rasionya adalah dengan membagi satu suku dengan suku sebelumnya.
Contoh:
Yang dikenal nomor 3, 9, 27, 81, 243, …. Berapakah nilai suku ke-8?
- kamuN = arn-1
- kamu8 = 3(38-1)
- kamu8 = 3(37)
- kamu8 = 3(2187)
- kamu8 = 6.561
5. Pola Kotak
Pola yang satu ini disebut pola persegi karena susunan bilangannya memiliki bentuk seperti persegi sehingga rumus ini juga memiliki rumus yang sama dengan persegi yaitu kuadrat. Sedangkan rumus pola pada persegi adalah :
kamuN = n2
Contoh susunannya adalah 1, 4, 9, 16, 25….
6. Pola Persegi Panjang
Pola ini hampir sama dengan pola persegi, namun memiliki rumus yang sangat berbeda. Jika sebelumnya angka-angka berbentuk seperti persegi, kali ini polanya akan membentuk susunan yang menyerupai persegi panjang.
Pola persegi panjang ini menghasilkan rumus:
kamuN = n(n+1)
Dari rumus di atas, salah satu contoh pola persegi panjang adalah 2, 6, 12, 20, dan seterusnya.
7. Pola Segitiga
Sama seperti pola sebelumnya, pola ini disebut segitiga karena susunannya menyerupai bentuk segitiga sama sisi. Untuk menemukan sukuN Dari pola ini, Anda dapat menggunakan rumus berikut.
kamuN = ½n (n+1)
Dengan menggunakan rumus diatas maka akan terbentuk pola segitiga seperti contoh 1, 3, 6, 10, dan seterusnya.
8. Pola Bilangan Fibonacci
Pola Fibonacci adalah pola yang terbentuk dari susunan bilangan yang dimulai dari angka 0 dan 1, kemudian diperoleh suku berikutnya dari penjumlahan dua suku sebelumnya. Contohnya adalah 0, 1, 1, 2, 3, 5, 8, dan seterusnya.
Untuk menghitungN maka Anda dapat menggunakan rumus berikut:
kamuN = (n-1) + (n-2)
9. Pola Segitiga Pascal
Terakhir, ada nomor yang disebut Pascal. Dinamakan demikian karena pola ini ditemukan oleh seorang ilmuwan Perancis bernama Blaise Pascal. Pola ini juga dikenal sebagai segitiga Pascal dengan kondisi di bawah ini:
- Baris paling atas hanya ditulis satu angka 1 saja
- Baris berikutnya mulai dari baris ke-2 hingga baris ke-2N diperoleh dari penjumlahan dua bilangan diagonal di atasnya.
- Setiap baris dalam segitiga Pascal harus dimulai dan diakhiri dengan angka 1.
- Setiap baris akan dibentuk secara simetris
- Banyaknya bilangan pada setiap baris merupakan kelipatan dua dari jumlah keseluruhan bilangan pada baris sebelumnya.
Dengan begitu, pada bilangan ini akan terdapat aturan geometri yang susunannya memuat koefisien binomial untuk membentuk segitiga. Contoh pola Pascal adalah 1, 2, 4, 8, 16, 24, dan seterusnya. Rumusnya adalah sebagai berikut:
kamuN = 2n-1
Contoh soal Pola Angka dan diskusi
Setelah mempelajari pengertian dan bentuk pola pada bilangan beserta rumusnya di atas, tentunya kurang lengkap jika tidak mempelajari contoh soal. Hal ini dikarenakan terdapat beberapa model masalah yang dapat diselesaikan dengan berbagai rumus yang cocok pula.
Untuk itu, berikut beberapa contoh soal beserta pembahasannya yang bisa kamu pelajari!
1. Contoh Soal Pola Geometri
Diketahui ada pola 32, 16, 8, 4, …. Berapakah suku ke-7 dari pola tersebut?
Diskusi:
- Diketahui: a = 32, r = 16/32 = ½, n = 7
- Ditanya: U7?
- Dijawab:
- kamuN = arn-1
- kamu7 = 32,1/27-1
- kamu7 = 32,1/26
- kamu7 = 32,1/64
- kamu7 = 32/64
- kamu7 = ½
Jadi, suku ke-7 dari bilangan di atas adalah ½.
2. Contoh Soal Pola Aritmatika
Mendefinisikan dua suku berikutnya nomor 3, 6, 9, 12 benar!
Pembahasan: Untuk soal seperti ini, penyelesaiannya bisa dilakukan secara manual karena hanya menentukan dua suku setelah suku terakhir. Metodenya adalah sebagai berikut:
- Cari selisihnya dengan mengurangkan U2 dengan mu1jadi 6-3 = 3
- Tentukan dua suku berikutnya dengan menjumlahkan 3 suku terakhir. 12 + 3 = 15, 15+3 = 18.
Jadi, dua suku berikutnya adalah 15 dan 18. Bagaimana caranya? Apakah Anda sekarang lebih mengerti tentang nomor beserta bentuk dan rumusnya? Selain itu jangan lupa untuk mencoba banyak soal latihan agar kamu bisa lebih memahami materi ini. Roh!
Baca Juga Artikel Lainnya :