Dalam Matematika, ada yang namanya barisan aritmetika dan deret aritmatika. Padahal, keduanya tidak dapat dipisahkan karena rangkaian dan deret tersebut saling terkait satu sama lain.
Aritmetika sendiri merupakan bagian dari Matematika yang membahas tentang operasi bilangan dasar yang meliputi pembagian, perkalian, pengurangan dan penjumlahan. Walaupun ada yang namanya sequence dan series, kali ini khusus menjawab pertanyaannya apa itu barisan aritmatika?
Pengertian Barisan Aritmatika

pendeknya, barisan aritmatika adalah urutan angka yang memiliki pola tetap. Pola yang dimaksud dapat dibentuk berdasarkan operasi pengurangan atau penjumlahan. Dengan demikian, setiap urutan suku kata akan memiliki perbedaan yang besarnya sama.
Nantinya perbedaan ini akan disebut perbedaan dan umumnya dilambangkan dengan huruf b. Dengan demikian, itu bisa diambil contoh barisan aritmatika sebagai berikut:
- Suku pertama adalah angka 2 dan biasanya dilambangkan dengan U1 atau yang secara matematis dinyatakan sebagai a
- Istilah kedua adalah angka 5 dan biasanya dilambangkan dengan U2
- Kemudian suku ketiga adalah angka 8 dan biasanya dilambangkan dengan U3 dan seterusnya
Melihat contoh-contoh di atas, dapat disimpulkan bahwa barisan aritmatika yang berurutan adalah 2, 5, dan 8. Melihat angka-angka tersebut, antara angka 2 dan angka 5 terdapat selisih 3 angka. Begitu juga dengan angka 5 dan angka 8 terdapat selisih 3 angka juga.
Macam-Macam Barisan Aritmatika
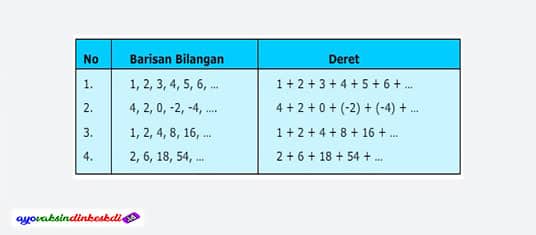
Perlu diketahui juga bahwa ada 2 jenis barisan aritmetika, yaitu barisan turun dan barisan naik. Urutan menurun adalah urutan angka yang nilai angkanya negatif atau menurun. Sedangkan jika barisannya turun, ini merupakan barisan bilangan yang nilai bilangannya positif atau bertambah.
Mari kita ambil contoh berikut agar lebih mudah dipahami:
- 7, 14, 21, 28, 35 (Misalnya antara angka 7 dan angka 14 selisihnya adalah 7, kemudian dari angka 14 ke angka 21 selisihnya adalah 7, dan dari angka 21 ke angka 28 selisihnya adalah 7, jadi dari angka 28 ke angka 35 selisihnya juga 7. Deret angka ini memiliki selisih yang bernilai 7 dan dari angka pertama ke angka terakhir terus bertambah atau bernilai positif, jadi barisan ini merupakan barisan menaik)
- 45, 40, 35, 30 (Misalnya dari angka 45 ke angka 40 ada selisih 5, lalu dari angka 40 ke angka 35 ada selisih 5, jadi dari angka 35 ke angka 30 ada selisih dari 5. Selisih setiap bilangan memang 5, tetapi dari bilangan pertama ke bilangan terakhir terjadi pengurangan sehingga nilainya negatif. Jadi barisan kedua ini merupakan barisan menurun)
Seperti yang dinyatakan sebelumnya, barisan aritmetika adalah barisan bilangan yang selisih angkanya sama. Selisih ini biasa disebut selisih sehingga jika nilai selisih (b) positif, maka barisan aritmetikanya naik.
Sebaliknya, jika selisih (b) negatif, maka barisan aritmetikanya berkurang. Sampai disini kamu sudah lebih paham tentang barisan aritmetika kan?
Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika Tingkat Mudah

Angka-angka yang disebutkan dalam urutan ini dapat disebut sebagai suku. Saat ada soal yang mengharuskan kamu mencari suku ke-n atau Un, daripada menghitung secara manual, kamu bisa menggunakan rumus agar lebih cepat. Rumus yang dimaksud adalah sebagai berikut.
- Rumus mencari suku ke-n:
kamuN = U1 + (n – 1)b atau UN = a + (n – 1)b
- Rumus mencari nilai selisih:
b = UN – Un-1
- kamuN = suku ke-n
- kamu1 /a = suku pertama
- kamun-1 = suku ke-n
- B = berbeda
- n = jumlah suku dalam deret
Dari rumus di atas, selanjutnya mari kita aplikasikan pada contoh soal berikut ini:
Pertanyaan: Ya barisan aritmetika sebagai berikut 3, 7, 11, 15, … Temukan suku ke-10 dari barisan tersebut!
Jawaban: Diketahui bahwa
kamu1 = a = 3
b = U2 – U1 = 7 – 3 = 4
n=10,
Jadi
kamuN = a + (n – 1)b
kamu10 = 3 + (10 – 1)4 = 39
Jadi dari soal di atas dapat diketahui suku ke-10 dari barisan tersebut adalah 39.
Rumus Barisan Aritmatika Lainnya

1. Rumus Cepat Mencari Suku ke-N
Soal dan penyelesaian di atas termasuk dalam kategori soal mudah. Hal ini dikarenakan istilah pertama dan perbedaan atau selisih dari masing-masing suku juga dapat diketahui dengan mudah. Akan tetapi, lain cerita bila ada soal yang suku pertamanya tidak diketahui, beserta perbedaan atau selisihnya.
Untuk soal seperti ini, sebenarnya ada rumus yang juga bisa digunakan untuk mempercepat perhitungan. Tentunya rumus yang dimaksud berbeda dengan rumus sebelumnya ya, dan cara menghitung barisan aritmatika dalam kasus seperti berikut.
- Rumus cepat untuk mencari suku ke-n
NSaya =Uni-Un1+(n1 .b)b
- Formula cepat untuk menemukan perbedaan atau perbedaan
b =Un2-Un1n2-n1
Informasi:
- kamun1 = suku yang diketahui dan n terkecil
- kamun2 = suku yang diketahui dan n adalah yang terbesar
- kamuni = suku yang dikenal tetapi suku yang masih belum diketahui
- b = berbeda
- n1 = suku terkecil
- n2 = suku terbesar
- ni = suku mana yang ditanyakan
Dengan menggunakan rumus ini, meskipun suku pertama dan selisih atau selisih barisan tidak diketahui, perhitungannya akan lebih mudah. Untuk lebih memahaminya, mari kita lihat contoh soal berikut.
Soal: Jika suku ke-3 adalah 8 dan suku ke-5 adalah 14, maka suku ke-2 adalah 29…
Jawaban: Diketahui Un1 = 8, Un2 = 14, n1 = 3 dan n2 = 5, maka
- Pertama, cari selisih atau selisih barisnya terlebih dahulu
b=Un2-Un1n2-n1 = 14-85-3 = 62 = 3
- Jika perbedaannya diketahui, maka tinggal mencari suku yang dimaksud
NSaya =Uni-Un1+(n1 .b)b =29-8 + (3 .3)3 =303 = 10
Jadi, diketahui bahwa 29 adalah U10 atau suku ke-10
2. Cara Mencari Suku Pertama Barisan Aritmatika
Ada juga pertanyaan yang akan meminta Anda menentukan suku pertama. Soal-soal seperti ini sebenarnya adalah soal-soal yang mudah asalkan Anda benar-benar memahami konsep dasar dan rumus-rumus dalam rangkaian ini. Jadi, kamu harus mengingat rumus sebelumnya yaitu Un = a + (n – 1)b.
Ambil contoh soal berikut.
Jika suku keempat adalah 55 dan suku ketujuh adalah 85 dan selisih deretnya adalah 10, maka suku pertamanya adalah?
Ada dua cara untuk menyelesaikan masalah seperti ini, yaitu dengan menyusun istilah yang diketahui (SPLDV) atau dengan menggunakan urutan yang berbeda. Kedua cara tersebut akan memberikan hasil yang sama.
Namun untuk contoh diatas mari kita selesaikan dengan menggunakan urutan yang berbeda karena cenderung lebih mudah. Maka pembahasannya adalah sebagai berikut.
Dikenal: U4 = 55, U7 = 85, dan b = 10
- Dengan menggunakan suku keempat sehingga n = 4
Un = a + (n – 1)b
U4 = a + (4 – 1)b
55 = a + 3b
55 = a + 3 (10)
a = 55 – 30 = 25
- Dengan menggunakan suku ketujuh sehingga n = 7
U7 = a + (7 – 1)b
85 = a + 6 (10)
A = 85 – 60 = 25
Jadi baik menggunakan suku terbesar maupun menggunakan suku terkecil hasilnya sama yaitu 25.
Jika suku kelima adalah 27 dan suku kesembilan adalah 39, tentukan suku pertama dari barisan tersebut!
Pada soal ini perbedaan barisan tidak diketahui dan ada tiga langkah penyelesaiannya sebagai berikut.
- Langkah 1 membuat persamaan untuk suku-suku yang diketahui
>> Untuk suku kelima atau n = 5
U5 = a + (5 – 1)b
27 = a + 4b
>> Untuk suku kesembilan atau n = 9
U9 = a + (9 – 1)b
39 = a + 8b
- Langkah 2 Selesaikan sistem persamaan linier yang telah dibentuk di atas baik dengan metode substitusi maupun dengan metode eliminasi. Untuk kali ini, metode substitusi akan digunakan.
>> Persamaan (1)
a + 4b = 27 dapat diubah menjadi a = 27 – 4b
>> Persamaan (1) disubstitusi ke persamaan (2)
39 = a + 8b
39 = 27 – 4b + 8b
4b = 39 – 27 = 12
b = 3
- Langkah 3, substitusikan nilai b di atas untuk mendapatkan nilai a, bisa menggunakan persamaan (1) atau menggunakan persamaan (2). Namun untuk pembahasan kali ini menggunakan persamaan (1).
a = 27 – 4b = 27 – 4(3) = 27 – 12 = 15
Dari ketiga langkah penyelesaian di atas, akhirnya diketahui bahwa suku pertama barisan tersebut adalah 15.
Barisan Aritmetika Bertingkat
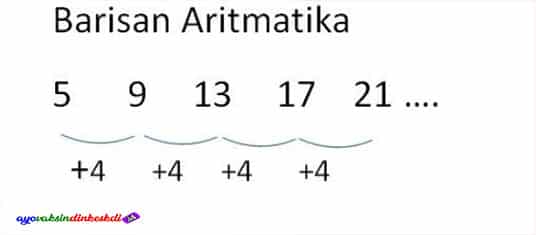
mudah, Urutan aritmatika bersarang adalah barisan yang nilai beda tetapnya tidak dapat ditemukan langsung pada level pertama sehingga harus dicari nilai selisihnya pada level selanjutnya. Dalam barisan berjenjang ini, ada banyak dari mereka yang naik ke tingkat kesepuluh dan seterusnya.
Jika nilai selisihnya masih dapat ditemukan pada deret tingkat pertama, maka disebut deret satu tingkat. Sedangkan jika nilai selisihnya masih dapat ditemukan pada deret tingkat kedua, maka disebut deret dua tingkat, dan seterusnya. Agar lebih mudah dipahami, mari kita lihat contoh berikut.
- Deret bilangan 1, 5, 12, 22, 35, … dari deret bilangan tersebut, Anda tidak dapat melihat nilai beda tetapnya bukan? Dari angka 1 ke angka 4 selisihnya 4, dari angka 5 ke angka 12 selisihnya 7, dari angka 12 ke angka 22 selisihnya 10, dan dari angka 22 ke angka 35 selisihnya 13
- Jadi, urutan di atas dengan selisihnya bisa ditulis seperti ini
1, 5, 12, 22, 35
4 7 10 13
- Nah, jika bilangan 4, 7, 10 dan 13 di atas dianggap sebagai barisan baru, akan terlihat bahwa antara suku pertama dan kedua, suku kedua dan ketiga dan seterusnya memiliki nilai selisih tetap 3 sehingga bisa menjadi seperti ini.
1, 5, 12, 22, 35
4 7 10 13
3 3 3
- Dalam hal ini, jika 4, 7, 10 dan 13 dianggap sebagai barisan derajat 1, maka suku baru yang sebenarnya merupakan hasil selisih barisan sebelumnya dianggap sebagai barisan derajat 2, maka nilainya dari perbedaan tetap dari urutan dianggap ditemukan di tingkat kedua.
Mempelajari barisan aritmetika Sekilas memang terlihat rumit. Namun jika Anda mengetahui konsep dan prinsip dasar serta mengingat rumusnya, maka materi ini tidak akan menjadi masalah lagi. Selain itu, untuk lebih mengasah kemampuan Anda, sering-seringlah berlatih mengerjakan soal.
Baca Juga Artikel Lainnya :
- Deret Aritmatika – Pengertian, Sejarah, Cara Menghitung, Contoh
- Soal Deret Aritmatika yang Perlu Anda Pelajari
- Notasi Sigma Kelas 11 – Definisi, Rumus, dan Contoh Soal
- Pola Bilangan Segitiga, Fibonacci, Ganjil, Kotak, Dll (Lengkap)
- Notasi Sigma Kelas 11 – Definisi, Rumus, dan Contoh Soal
- Ciri-Ciri Pangkat Beserta Pengertian, Sifat & Contoh Soal
- Tabel Periodik Unsur Kimia dan Deskripsi Lengkap PDF