Jika Anda berada di kelas X SMA, Anda mungkin pernah menerima materi pelajaran matematika tentang fungsi invers. Kata inverse berasal dari bahasa Inggris dan memiliki arti sebaliknya. Artinya, fungsi yang memiliki fungsi kebalikan dari fungsi aslinya dan dilambangkan dengan f^(-1).
Selain digunakan dalam perhitungan fungsi, invers dalam Matematika juga digunakan untuk menghitung matriks. Seperti halnya fungsi pada materi Matematika lainnya, invers juga memiliki rumus yang digunakan dalam perhitungan.
Jika dilihat dari rumusnya saja, mungkin materi invers ini akan terlihat rumit, padahal tidak. Perhitungan invers dapat dilakukan dengan mudah, asalkan konsep dasarnya dipahami terlebih dahulu.
Definisi Fungsi Invers

Tadi telah disebutkan bahwa fungsi invers adalah kebalikan dari fungsi semula. Namun ternyata tidak selalu demikian seperti yang dijelaskan dalam buku “Modul Pembelajaran Matematika Umum Kelas X SMA”.
Dalam buku teks Matematika karangan Entis Sutisna, invers suatu fungsi tidak selalu menghasilkan fungsi. Ada syarat yang harus dipenuhi agar suatu invers dapat menghasilkan suatu fungsi, yaitu jika f satu-satunya korespondensi atau merupakan fungsi bijektif dari invers tersebut.
Penjelasan Fungsi Bijektif dan Fungsi Satu-ke-Satu
Untuk lebih memahami tentang fungsi bijektif dan fungsi satu-ke-satu pada invers, Anda dapat melihatnya pada contoh berikut.
Dari grafik di atas dapat dijelaskan sebagai berikut:
- Fungsi bijektif dapat terjadi ketika semua anggota kodomain memiliki mitra dalam domain tersebut. Sederhananya, dalam fungsi bijektif semua anggota dalam domain dan kodomain memiliki pasangan.
- Jamur invers satu-ke-satu adalah semua anggota domain memiliki mitra dari codomain. Singkatnya, fungsi satu-ke-satu dapat meninggalkan satu anggota domain yang tidak dipasangkan dengan anggota kodomain.
Invers dari suatu fungsi adalah
Sebelum berbicara dan membahas lebih lanjut tentang rumus terbalik dan cara menghitungnya, kita lihat dulu Apa invers dari suatu fungsi. Secara etimologi, invers berarti fungsi yang berlawanan dengan fungsi asalnya.
Secara umum, yang memiliki simbol (f) hanya dapat memiliki invers (f-1) jika fungsinya menjadi satu dan juga fungsi bijektif. Apa itu fungsi bijektif? Yang dimaksud dengan merupakan fungsi bijektif bila jumlah domain sama dengan jumlah anggota kodomain.
Lalu apa pengertian domain dan kodomain? Pengertian domain adalah asal, dan kodomain berarti daerah hasil. Dari pengertian domain dan kodomain, fungsi (f) akan memetakan A ke B, dan fungsi invers sebaliknya, yaitu B ke A.
Jadi, jika fungsi (f) : A🡪B telah ditentukan dengan menggunakan aturan y = f(x), maka dapat dituliskan sebagai: invers (f-1) = B🡪A, dengan aturan yang digunakan adalah x = f-1 (y).
Jadi, jika Anda ingin menentukan inversnya, maka Anda harus melalui langkah-langkah berikut ini.
- Ubah dulu bentuk y = f(x) menjadi kebalikannya, yaitu x = f(y)
- Selanjutnya Anda menulis x dengan f-1jadi kita mendapatkan persamaan dengan rumus f-1 (y) = f(y)
- Kemudian ubah variabelnya, yaitu x menjadi y, sehingga pada persamaan terakhir diperoleh f-1(x) = f(y)
Matriks Invers Adalah
Selain digunakan untuk menghitung, invers juga digunakan dalam perhitungan matriks. Apa yang dimaksud dengan invers matriks? Pengertian invers matriks adalah kebalikan dari matriks, dimana jika matriks tersebut dikalikan dengan inversnya maka hasilnya adalah matriks identitas.
Suatu matriks dapat memiliki invers jika determinan matriks tersebut tidak sama dengan 0 (nol). Bagaimana cara menentukan invers matriks? Anda dapat menghitungnya menggunakan urutan referensi 2 × 2 atau 3 × 3.
Rumus menghitung invers matriks dengan orde 2×2 adalah:
Mengacu pada rumus di atas, jika ingin mengetahuinya Berapa invers dari matriks berorde 2×2 adalah sebagai berikut :
- Tukar elemen pada diagonal utama.
- Beri atau tambahkan tanda (-) pada setiap elemen lainnya.
- Setelah itu, lakukan pembagian pada setiap elemen matriks dan determinannya.
Adapun rumus matriks orde 3×3 adalah sebagai berikut:
Cara menghitung invers matriks dengan orde 3×3 dapat dilakukan melalui 2 metode, yaitu adjoin dan transformasi baris elementer. Apa artinya berdampingan? Pengertian dari bersebelahan adalah transpos matriks di mana elemen adalah kofaktor dari elemen matriks.
Fungsi Invers Matriks
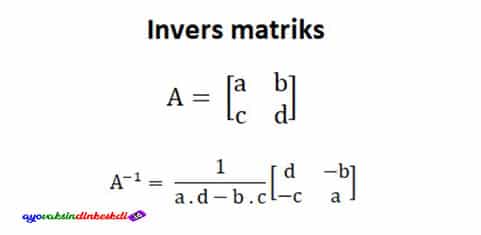
Bagaimana dengan invers matriks? Invers matriks memiliki fungsi untuk menyelesaikan masalah dalam matriks. Sebelum menggunakan rumus invers matriks, hal pertama yang harus dilakukan adalah mengetahui determinan terlebih dahulu.
Apa itu penentu? Definisi determinan adalah nilai yang dapat dihitung melalui elemen matriks persegi. Invers matriks adalah invers dari kedua matriks tersebut.
Jika matriks tersebut dikalikan maka akan menghasilkan matriks persegi yang dilambangkan dengan (AB = BA = │). Simbol matriks investasi adalah pangkat -1 yang ditempatkan di bagian atas huruf, yaitu f-1.
Rumus Fungsi Invers
fungsi invers adalah fungsi dalam Matematika yang berarti kebalikan dari fungsi aslinya. Sesuatu yang dilambangkan dengan (f) hanya dapat dikatakan memiliki invers (f-1) jika memenuhi persyaratan seperti yang dijelaskan sebelumnya.
Suatu fungsi hanya akan memiliki invers jika merupakan fungsi bijektif atau fungsi satu-ke-satu, seperti dibahas di atas. Dari situ akan didapatkan relasi fungsi menjadi sebuah rumus:
f = (f-1)-1
Adapun rumus lengkap fungsi invers adalah sebagai berikut :
Selain rumus fungsi invers seperti di atas, masih ada rumus dengan komposisi. Rumus invers dengan fungsi komposisi dapat dilihat di bawah ini.
Fungsi Komposisi Invers
Diatas sudah dituliskan rumus fungsi invers komposisi, agar lebih memahaminya akan dibahas sedikit tentang pengertiannya. Fungsi adalah hubungan himpunan A dengan himpunan B, dimana setiap anggota himpunan A dipasangkan dengan salah satu anggota himpunan B.
Himpunan A adalah domain dan himpunan B disebut kodomain. Ada dua macam hubungan antara himpunan A dan B, yaitu komposisional dan invers. Apa yang dimaksud dengan fungsi komposisi?
Fungsi komposisi adalah kombinasi dua fungsi, f(x) dan g(x) dan memiliki simbol “o”, yang dibaca sebagai bundaran atau komposisi (lihat rumus di atas).
Memahami fungsi komposisi yang lainnya adalah keadaan di mana dua fungsi digabungkan secara berurutan untuk membentuk fungsi baru. Penggabungan kedua fungsi f(x) dan g(x) akan membentuk fungsi baru, yaitu:
Cara membaca rumus di atas adalah (kabut) dibaca sebagai “fungsi bundaran g”. Mengacu pada rumus, maka g akan dilakukan terlebih dahulu baru kemudian melakukan fungsi f. Berbeda dengan rumus kedua dimana (gof) yang berbunyi “fungsi bundaran f”, maka f dikerjakan terlebih dahulu baru g.
Setelah itu akan diketahui fungsi invers perhitungan ini, yaitu fungsi kebalikan dari aslinya. Jika bentuk aslinya adalah fungsi f maka inversnya adalah f-1.
Fungsi komposisi ini memiliki ciri tertentu yang membedakannya dengan fungsi lainnya. Sifat komposisi terbalik diantaranya adalah:
- Sifat komutatif tidak berlaku
- Sifat yang berlaku adalah asosiatif
- Memiliki unsur identitas.
Simbol Fungsi Invers
Setelah pembahasan yang cukup panjang di atas, apakah anda paham apa itu simbol fungsi invers dan kegunaannya? Benar jika Anda menjawab lambang invers pangkat -1 (-1) ditulis setelah huruf.
Misalnya matriks X adalah invers dari matriks Y, dapat ditulis dengan simbol :
X = Y-1 (y-1)
Sedangkan jika matriks Y merupakan invers dari matriks X, maka lambangnya ditulis sebagai berikut:
Y = X-1 (x-1)
Dari penjelasan dan rumus di atas dapat disimpulkan bahwa matriks X dan Y merupakan dua matriks yang saling invers atau invers.
Contoh Soal Fungsi Invers
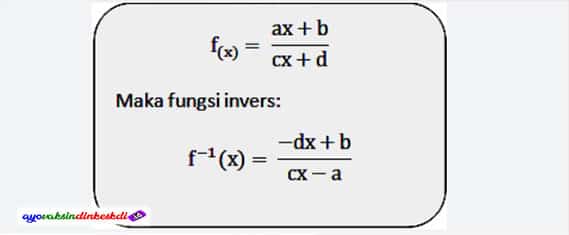
Sekarang Anda seharusnya sudah mulai memiliki sedikit gambaran tentang invers dan fungsinya. Sekali lagi, Anda harus selalu ingat bahwa yang dimaksud dengan invers menurut bahasa adalah kebalikan. Sedangkan pengertian terbalik berarti kebalikan dari fungsi aslinya.
Agar lebih jelas, Anda dapat melihat contoh soal berikut ini.
1. Klub sepak bola memiliki sumber pendapatan dari penjualan tiket penonton saat ada pertandingan. Besaran dana tergantung berapa banyak penonton yang menyaksikan pertandingan tersebut.
Sebuah klub sepak bola membocorkan informasi bahwa jumlah pendapatan yang diperoleh klub dari penjualan tiket mengikuti rumus fungsi f(x) = 250X + 15.000, dimana X adalah jumlah penonton yang membeli tiket pertandingan sepak bola.
Berapa kebalikan pendapatan dari penjualan tiket untuk penonton?
Cara melakukannya adalah:
- Buatlah contoh f(x) = y
- Hitung f(x) 🡪 f(x) = 250X + 15.000
- Setelah itu tentukan rumus f^(-1)(y) = x
- Ganti variabel y dengan x
- Mulailah melakukan perhitungan sesuai rumus yaitu:
y = 250X + 15.000
= -250X = y – 15.000 (dikalikan -1)
= 250X = y – 15.000
= X = (y – 15.000) / 250
= f^(-1) (x) = (X – 15.000)/250
2. Diketahui f : B -🡪 B dengan f(x) = 3X – 7, tentukan nilai f^(-1) (X) dari fungsi tersebut.
Cara melakukannya menggunakan tahapan berikut:
- Misal f(x) = y 🡪 f(x) = 3X – 7 ubah menjadi y =3X – 7
- Tentukan rumusnya, yaitu f^(-1) (X) dan ingat bahwa f^(-1) (y) = x, dan ganti variabel y dengan x.
Membuat perhitungan, yaitu :
y = 3X – 7
= 3X = y + 7
= X = (y+7)/2
= f^(-1) (x) = (y+7)/2
Dari kedua contoh di atas, Anda bisa melihat cara mengetahui invers suatu fungsi beserta langkah-langkah menghitungnya sesuai dengan rumusnya.
Demikianlah pembahasan tentang terbalik dalam mata pelajaran Matematika yang juga menjadi mata pelajaran bagi siswa kelas X SMA. Meski terlihat rumit, sebenarnya invers tidak sesulit yang dibayangkan, asalkan Anda memahami konsepnya.
Anda hanya perlu selalu ingat bahwa kata invers memiliki arti kebalikan, jadi fungsi invers adalah fungsi yang kebalikan dari asalnya. Setelah itu pahami bagaimana rumus dan langkah-langkah menentukan nilainya, semudah itu. Selamat belajar, semoga sukses.
Baca Juga Artikel Lainnya :
- Fungsi Komposisi dan Fungsi Invers dengan Contoh Soal
- Fungsi Dinding Sel Tumbuhan, Bakteri, Jamur, Alga Dll
- Contoh soal kaliper beserta fungsi dan jenisnya
- Cara Menghitung Persen di Excel, Kalkulator, Rumus, Contoh Soal
- Contoh Limit Fungsi Aljabar dan Jawabannya
- Rentang Penyimpangan Kuartil, Jenis, Cara Mencari, Contoh Soal
- Bilangan dengan Pangkat Pecahan, Bentuk Akar, dan Contoh Soal