Ayovacsindinkeskdi.id – Pernahkah kamu merasa kesulitan menghitung jumlah deretan angka dalam rumus matematika? Jika iya, mungkin Anda perlu mempelajari notasi sigma untuk menyederhanakan bilangan tersebut. Agar mudah dipahami, berikut penjelasannya.
Apa itu Notasi Sigma?
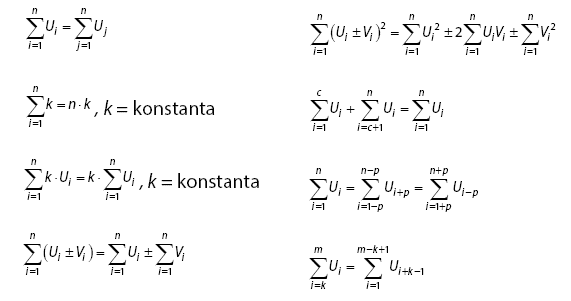
Materi matematika dasar ini disebut juga notasi penjumlahan. Sangat penting untuk Anda ketahui untuk dapat mempelajari dasar-dasar matematika lanjutan seperti kalkulus dan statistika. untuk mengenalnya lebih dalam setelah ulasannya.
Memahami
Notasi sigma secara sederhana didefinisikan sebagai penjumlahan. Rumus ini digunakan untuk menyingkat rangkaian penjumlahan bilangan agar tidak terlalu panjang. Materi ini masih berkaitan erat dengan deret aritmetika dan geometri.
dalam sains pendidikan Materi matematika ini digunakan sebagai penjumlahan deret bilangan. Dimana hasilnya adalah penjumlahan dari penjumlahan tersebut. Tidak hanya bilangan, bentuk lain yang bisa dijumlahkan adalah vektor, fungsi, matriks, dan polinomial.
Adder dimulai dari urutan eksplisit dan dilambangkan sebagai suksesi penambahan. Adanya penjumlahan asosiatif dan komunikatif sehingga tidak memerlukan tanda kurung dan besarannya tidak bergantung pada urutan puncak.
Penjumlahan ini dimulai dari urutan satu elemen yang menghasilkan elemen itu sendiri. Misalnya, jika penjumlahan dimulai dengan barisan elemen 0, maka konversinya adalah 0. Sedangkan untuk pola sederhana penjumlahan deret panjang diganti dengan elips.
Contoh penjumlahan 100 bilangan asli dapat dituliskan sebagai 1 + 2 + 3 + 4 + …. + 100. Untuk menyederhanakan rumus, gunakan rumus sigma dengan simbol Σ. Simbol ini adalah huruf Yunani yang disebut “sum” yang berarti penjumlahan.
Rumus notasi penjumlahan ini ditulis dalam bentuk berikut:
Jumlah n bilangan asli pertama dilambangkan dengan i-1n1
Rumus Notasi Modal Sigma

Dengan konsep yang sama, notasi sigma kapital menggunakan simbol di atas untuk menyatakan penjumlahan dari banyak suku atau deret bilangan. Rumusnya ditulis sebagai i-mnai = am+ am+i + + an – 1 + an.
Dalam rumus di atas, i adalah indeks penjumlahan. Sedangkan ai adalah variabel indeks untuk setiap suku dari jumlah yang ditambahkan. m adalah simbol batas bawah penjumlahan dan n adalah batas atas penjumlahan.
Sedangkan i=m adalah simbol penjumlahan yang menunjukkan indeks dimulai dengan m, dan i adalah kenaikan setiap suku dan diakhiri dengan i=n. Berikut adalah contoh penjumlahan bilangan kuadrat.
i=24i2= 22 + 32 + 42 = 29
Terkadang dalam penulisan informal definisi indeks dan batas penjumlahan dihilangkan. Ini benar jika jelas dalam konteksnya. Misalnya pada rumus berikut: ai= i=mnai. Selain itu ada juga generalisasi notasi dimana kondisi arbitrer disediakan.
Berikut adalah beberapa contoh yang paling sering ditemui:
- 0 k sebagai kisaran yang ditentukan.
- x∈Sfx adalah jumlah f(x) yang memuat semua anggota x dalam himpunan S
- dln(d) adalah jumlah dari (d) untuk bilangan positif d dibagi dengan n.
Perubahan Rumus Notasi Sigma
Apakah kamu tahu? bahwa notasi penambahan memiliki berbagai bentuk. Mulai dari perubahan indeks, serta penulisan notasinya. Berikut ini lebih jelas.
1. Perubahan indeks
Yang menarik dari notasi penjumlahan adalah indeksnya dapat diubah sesuai kebutuhan. Sehingga dalam penulisan indeks tidak harus selalu menggunakan huruf i. Anda dapat menggunakan huruf lain seperti a, l, atau k.
Namun, saat mengubahnya, pastikan indeks dalam matematika juga diubah dengan huruf yang sama. Sedangkan huruf yang digunakan untuk menyatakan batas atas notasi penjumlahan tidak sama dengan huruf pengganti pada indeks sigma. Contohnya adalah sebagai berikut:
i=1ni = a=1na
Dari bentuk rumus diatas kita dapat mengetahui indeks pada rumus sebelumnya dengan menggunakan huruf i. Kemudian diganti dengan huruf “a” dengan catatan kalimat matematika pada rumus menggunakan huruf yang sama sesuai indeks.
Walaupun hurufnya sudah berubah, kedua rumus sigma tersebut tetap memiliki nilai yang sama dan tidak berubah. Sehingga pada rumus di atas menggunakan simbol “sama dengan” untuk menyatakan bahwa kedua rumus sigma tersebut sama.
2. Perubahan notasi
Notasi pada rumus sigma juga dapat diubah seperti indeks. Untuk mengubah notasi pada sigma, ada dua cara yang bisa dilakukan. Yang pertama dipisahkan menjadi jumlah dua atau lebih notasi sigma dan yang kedua adalah dengan memisahkan suku pertama dan suku terakhir.
- Dipisahkan menjadi Sum
Notasi pada sigma dapat dipisahkan atau dipecah menjadi sejumlah penjumlahan dari beberapa rumus sigma. Untuk mengetahuinya, berikut adalah contoh perubahan notasi yang pertama:
i=1nui = i=1kui=k+1nui
Dari contoh di atas, kita dapat memecah rumus menjadi dua notasi. dari rumus sigma pertama batas atasnya adalah huruf n dengan indeks 1. Kemudian rumus kedua menghasilkan indeks k+1, dengan nilai indeks harus berurutan jika ingin dijumlahkan.
Sehingga ketika dipecah menjadi lebih dari dua penjumlahan, maka nilai indeks dan notasinya dijumlahkan secara berurutan. Ini karena semua nilai dalam rentang batas atas dan bawah harus dijumlahkan.
Penggunaan kalimat matematika pada rumus sigma juga harus sama dengan contoh di atas. dimana pada bagian rumus tertulis uSaya sehingga pada rumus pecahan rumusnya tetap sama tidak berubah.
Berikut adalah contoh mengubah notasi pada rumus sigm:
i=312i= i=38i+i=912i
i=312i= 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 75
i=38i= 3 + 4 + 5 + 6 + 7 + 8 = 33
i=912i= 9 + 10 + 11 + 12 = 42
Jadi jika dijumlahkan i=38i + i=912i hasilnya 75.
Jadi dalam mengubah indeks ini harus memperhatikan batas atas dan batas bawah harus memiliki nilai yang berurutan. Selain itu, kalimat pada rumus sigma pecahan harus sama dalam penggunaan simbolnya.
- Pemisahan Suku Pertama dan Terakhir
Berbeda dengan cara kedua, pengubahan bentuk rumus dilakukan dengan cara memisahkan suku-suku dalam rumus notasi sigma. Untuk mengetahuinya, berikut adalah contoh rumus yang digunakan.
i=1nui= i=1n-1u1Un
Kita dapat mencoba rumus di atas pada contoh berikut:
i=1n-13i+9= i=1n-13i + 9 + (3n + 9)
Maka solusinya adalah sebagai berikut:
i=3n-13i + 9= 3 + 9 + 6 + 9+9 + 9+…+3n-1+ 9+(3n + 9)
Kemudian kita ambil suku terakhir yaitu (3n+9) maka hasilnya adalah:
3 + 9 + 6 + 9+9 + 9+ + 3n-1+ 9= i=3n-13i + 9 , setelah itu kita kembalikan suku terakhir ke dalam bentuk penjumlahan.
i=3n-13i+9 +3n+9= i=3n3i+9
Ciri Notasi Sigma
Untuk mengenal sifat-sifat notasi penjumlahan, Anda dapat memperhatikan beberapa contoh soal di bawah ini.
- k=515003
- k=182k
- k=210(k2+ 2k)
- k=33(k3+6)
- k=412(k+3)
- k=1001 1006(3k+2)
Inilah solusinya:
Properti pertama dari rumus sigma adalah k=mn c = (n – m + 1)
k=515003= 3 + 3 + 3 + 3 + + 3
k=51500 3 =(1500-5+1)
k=51500 3 = 1496,3
k=51500 3 = 4488
Soal nomor dua dapat diselesaikan dengan menggunakan rumus sifat kedua, yaitu k=mncak=c × k=1nak. Maka solusinya adalah sebagai berikut:
k=182k= 2 k=18k
k=18 2k=2 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8)
k=18 2k =2 36
k=18 2k= 72
Untuk mengerjakan soal nomor tiga, kamu bisa menyelesaikannya dengan menggunakan sifat ketiga dari rumus sigma. Berikut rumus persamaan k=1n (ak+bk) = k=mnbk.
k=210k2 + 2k=( k=210k2 + k=2102k)
k=210k2 + 2k= 22+ 32+ 42+ 52+ 2k=210k
k=210k2 + 2k= 4 + 9 + 16 + 25 + 3 ×(2 + 4 + 5 + 6 + 7 + 8 + 9 + 10)
k=210k2 + 2k= 53 + 3 (51)
k=210k2 + 2k= 206
Sedangkan pada soal nomor 4 dapat menggunakan sifat-sifat rumus sigma k=nn ak = 0. Sehingga hasil dari k=33 (k3 + 6) =0
Pada soal kelima, Anda dapat menggunakan sifat-sifat rumus sigma k=m nak= k=mp-1ak + k=10nak. Maka solusinya adalah sebagai berikut.
k=412k + 3= k = 46k + 3 + k = 710k + 3
Kamu bisa menyelesaikan soal keenam dengan menggunakan rumus k=mnak = k=m=pn-pak+p . Inilah solusi untuk masalah ini.
k = 10011006(3k + 2)= k=1001-10001006-1000[5k +1000 +2]
k = 10011006(3k + 2)=k=16(3k+ 3002)
Contoh Soal dan Jawaban Notasi Sigma
Untuk lebih menguasai materi notasi sigma tentunya anda perlu berlatih dan mengetahui lebih dalam tentang rumus sigma. Berikut adalah beberapa contoh soal yang bisa Anda lihat beserta rumus penyelesaiannya.
pertanyaan pertama
Jika nilai k=121k=x, berapakah nilai k=100310213k-1995?. Untuk mengatasinya anda bisa menggunakan rumus sifat ketiga.
k= 100310213k – 2999= k=1003-10001021-1000(3(k +1000)-2999)
k= 100310213k – 2999= 3213k+3000-2999
k= 100310213k – 2999= 3213k + 1
Kemudian Anda dapat menerapkan properti pertama dan kedua sebagai berikut.
k = 100310213k – 2999= k = 3213k +3211
k = 100310213k – 2999= 3 k = 321k+20-3+3 . 1
k = 100310213k – 2999= 3k + 20
Pertanyaan 2
Nilai untuk i=150(2i + i2)=X sedangkan m=150(2m + m2)=Y. Bagaimana konsep hubungan antara M dan N? Solusinya adalah sebagai berikut.
Berdasarkan sifat rumus sigma:
k = mnak = j = mnaj
Pada contoh soal ini, kedua rumus memiliki batas bawah yang sama, yaitu 1 dengan nilai n = 50. Walaupun memiliki variabel yang berbeda pada bagian fungsinya, keduanya memiliki bentuk yang sama. Jadi dapat disimpulkan bahwa M sama dengan N.
Materi notasi sigma ini dapat dikembangkan menjadi berbagai rumus lainnya. Jadi sangat penting bagi Anda untuk mempelajari konsep dasarnya terlebih dahulu. Agar dapat menerapkannya saat berhadapan dengan rumus yang lebih rumit.
Untuk menguasai rumus notasi sigma dengan lebih baik, Anda bisa berlatih secara konsisten. Dengan mengerjakan berbagai soal latihan dan memahami konsep dengan baik dalam menentukan rumus penyelesaiannya.
Baca Juga Artikel Lainnya :
- Fungsi caliper, cara pakai, contoh soal dll
- Pola Bilangan Segitiga, Fibonacci, Ganjil, Kotak, Dll (Lengkap)
- Ciri-Ciri Pangkat Beserta Pengertian, Sifat & Contoh Soal
- Bilangan dengan Pangkat Pecahan, Bentuk Akar, dan Contoh Soal
- Kuantitas Turunan Bersama Satuan, Dimensi, dan Contoh
- Soal Deret Aritmatika yang Perlu Anda Pelajari
- Kumpulan Soal dan Kunci Jawaban PAS Kelas 3 SD Tema 2
- Soal PAS Kelas 1 SD Semester 1 Kurikulum Merdeka Tema 1-4
- Soal dan Kunci Jawaban PAS Kelas 4 SD Tema 2 Terbaru 2023
- Contoh Soal UAS IPA Kelas 9 Semester 1 + Kunci Jawaban