Fungsi komposisi merupakan bagian dari pelajaran matematika untuk anak SD dan SMP. Fungsi adalah relasi himpunan atau grup, misalnya dilambangkan dengan A, dengan grup atau himpunan dilambangkan dengan B.
Setiap anggota dari kelompok A dapat dipasangkan dengan anggota dari kelompok B. Dalam penerapannya dapat dikatakan sebagai fungsi. Satu fungsi yang terbentuk dapat dilanjutkan dengan fungsi lainnya.
Ini dapat membentuk fungsi baru bernama fungsi dan komposisi. Fungsi ini merupakan hasil dari dua fungsi yang telah digunakan sebelumnya. Fungsi ini juga dapat disajikan dalam bentuk rumus, diagram panah, pasangan terurut, dan diagram Cartesian.
Sejarah Munculnya Fungsi Komposisi

Pada awalnya fungsi ini muncul sejalan dengan perkembangan matematika. Awalnya dikenal dengan rangkaian abstrak sederhana yang selalu berlipat ganda dan merupakan perpanjangan dari materi pelajaran.
Abstraksi ini awalnya diterapkan pada hewan dan angka. Misalnya, ada dua jenis hewan seperti ayam dan sapi yang jumlahnya sama. Selanjutnya ayam dan sapi tersebut tentunya dimasukkan ke dalam kandang yang berisi kunci. Kemudian persamaan dihitung menjadi f(key).
Selain itu, gudang untuk menyimpan makanan, beras, susu, dan sebagainya juga menggunakan kunci sehingga sering diekspresikan dengan fungsi (f). Hanya saja peristiwa ini tidak tercatat dan tercatat dalam sejarah.
Rekaman paling awal dari fungsi dan persamaan adalah pada tahun 1350-an yang direkam oleh Oresme. Dia memiliki gagasan fungsi dependen dan independen pada variabel dalam jumlah barang.
Selanjutnya, selama revolusi industri, Gottfried Leibniz menerbitkan teori fungsi. Belakangan teori ini menjadi cikal bakal adanya kalkulus yang disempurnakan oleh matematikawan lain. Sejarah dalam matematika saling berhubungan satu sama lain.
Selain itu, pengetahuan ini memungkinkan adanya tumpang tindih teori satu sama lain sehingga tidak dapat dibuat garis waktu yang jelas. Ada beberapa tokoh lain yang berkaitan dengan fungsi, yaitu Johann Bernoulli, Leonhard Euler, Skolem, dan lain-lain.
Memahami Fungsi Komposisi
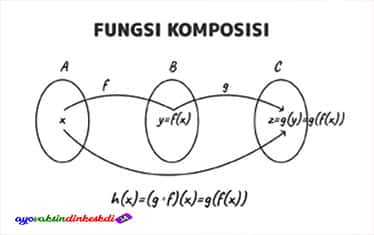
Fungsi dalam komposisi dapat diartikan sebagai pemetaan dari setiap anggota himpunan asal (domain) ke anggota himpunan hasil (kodomain). Ada juga beberapa istilah penting yang harus dipahami terkait dengan fungsi dan komposisi ini.
Beberapa istilah tersebut adalah komposisi yang artinya susunan. Sedangkan pemetaan adalah relasi atau relasi. Dalam konteks suatu hubungan, tentunya melibatkan lebih dari satu objek.
Domain adalah set asli. Sedangkan codomain adalah himpunan hasil. Oleh karena itu, dapat disimpulkan bahwa fungsi ini merupakan materi yang mempelajari cara mencocokkan himpunan asli dengan himpunan hasil.
Fungsi juga bisa dikatakan sebagai gabungan operasi antara 2 jenis fungsi yang ada. Sebaiknya Anda mengenal lebih dalam apa yang dimaksud dengan fungsi sebelum membahas lebih jauh tentang fungsi dan komposisi.
Ada dua jenis fungsi yang harus dipahami yaitu fungsi komposisi dan juga fungsi invers. Fungsi dan komposisi merupakan gabungan dari dua fungsi, yaitu domain dan kodomain. Jika dibuat rumus fungsi, maka dapat dilambangkan dengan f(x) sebagai domain.
Dan kemudian g(x) sebagai kodomain. Kedua fungsi ini digabungkan dan dilambangkan dengan “o”. Simbol kombinasi ini disebut komposisi. Susunan tersebut juga biasa disebut bundaran menurut simbolnya.
Formulasi Komposisi
Fungsi yang terbentuk adalah f(x) dan g(x) dan jika digabungkan menjadi (fog)(x) artinya koefisien g akan dimasukkan ke dalam f. Sedangkan kebalikannya (gof)(x) berarti koefisien f termasuk dalam g.
Sedangkan fungsi tunggal adalah fungsi yang dapat dilambangkan dengan huruf, misalnya gof dapat dibaca g bundaran f. Berbeda dengan fungsi invers yang memiliki arti fungsi invers.
Sehubungan dengan pembahasan tentang relasi dan juga fungsi, himpunan yang terlibat dapat diklasifikasikan menjadi 3 jenis daerah. Pertama adalah himpunan asal (domain), kemudian himpunan pengiring (kodomain), dan juga himpunan hasil (rentang).
Fungsi Invers
Result set ini merupakan hasil akhir dari pemetaan antar domain dan juga kodomain. Invers fungsi juga dapat muncul dari fungsi yang dilambangkan dengan f(x) dan kemudian memiliki hubungan antara himpunan A dan juga B.
Fungsi invers dapat dilambangkan dengan f – 1(x) karena relasinya dari himpunan B ke himpunan A. Fungsi ini diperoleh dari f: dari A ke B dan f-1 dari B ke A. Sehingga nantinya domain ( domain) f( x) akan menjadi area kawan.
Begitu juga sebaliknya, area kodomain akan menjadi area hasil atau f-1(x) dapat berupa himpunan. Hal ini juga berlaku untuk himpunan B. Fungsi invers atau fungsi balikan adalah fungsi yang merupakan kebalikan dari fungsi semula.
Jika f adalah satu-satunya fungsi dan dapat juga dikatakan sebagai fungsi bijektif. Hubungan ini dapat dinyatakan sebagai (f – 1) – = f. Pada fungsi ini, jumlah anggota pada domain harus sama dengan jumlah anggota pada kodomain.
Tidak ada lagi anggota di domain atau kodomain apa pun. Setiap anggota akan memiliki pasangan dalam hubungan mereka.
jenis Fungsi Komposisi

Ada 2 jenis fungsi utama yaitu f bundaran g dan juga bundaran g f. Maknanya akan dibahas lebih detail pada pembahasan berikut.
1. (gof) (x)
Cara membaca fungsi di atas adalah g roundabout f atau fungsi g komposisi f. Ini berarti bahwa fungsi tersebut dipetakan ke fungsi f(x) dan kemudian dipetakan oleh fungsi g (x).
Anda dapat memilih untuk mengerjakan fungsi f terlebih dahulu, kemudian melanjutkan mengerjakan fungsi g. Notasinya adalah sebagai berikut (gof)(x) = g (f(x)).
Jika melihat ilustrasi diagram panah, maka dapat digambarkan sebagai berikut.
2. (kabut) (x)
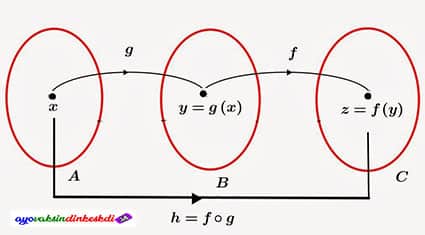
Cara membaca (kabut) (x) adalah dengan mengatakan f bundaran g atau fungsi f komposisi g. Artinya, fungsi g(x) dipetakan terlebih dahulu, lalu dilanjutkan dengan pemetaan fungsi f(x).
Anda dapat melakukan fungsi pemetaan g terlebih dahulu dan hasilnya dimasukkan ke dalam fungsi f. Hasil yang diperoleh adalah (kabut) (x) = f (g(x)).
Jika melihat ilustrasi diagram panah, maka dapat digambarkan sebagai berikut.
Ciri Fungsi Komposisi
Ada 3 ciri utama fungsi dan komposisi yang akan dijelaskan lebih jelas pada ulasan di bawah ini. Fungsi ini memiliki berbagai sifat menarik yang mencirikan sifatnya sehingga tidak bisa digunakan sembarangan.
1. Tidak ada sifat komutatif (fog)(x) ≠ (gof)(x)
Artinya, jika fungsi ini dibalik, maka tidak akan memiliki arti yang sama. Misalnya, dapat dibandingkan dengan perkalian. Jika 2 x 5 = 10. Maka 5 x 2 = 10 juga mendapatkan hasil yang sama. Berbeda dengan fungsi komposisi yang tidak menerapkan properti ini, karena hasilnya akan berbeda.
2. Berlaku sifat asosiatif yaitu fungsi (fo (goh))(x) = ((fog) oh)(x)
Artinya jika ada 3 fungsi komposisi, f disusun dengan g. Jadi, g terdiri dari h. Anda juga bisa melakukan compositing antara fungsi g dan h terlebih dahulu. Kemudian f mengarang dengan hasil kedua komposisi tadi.
3. Terdapat elemen identitas (I)(x), (fo I)(x) = (I of)(x) = f(x)
Artinya, fungsi f dan fungsi I memiliki identitas yang sama. Identitas ini untuk memastikan bahwa fungsi depan dan fungsi belakang benar-benar memiliki satu ciri yang berbeda. Keduanya tidak dapat digabungkan atau disusun secara sewenang-wenang.
Contoh Soal 1
Jika diketahui fungsi f(x) = 2x + 5 dan g(x) = 3x – 7, maka tulislah persamaan fungsi (fog)(x)
Menjawab:
Dikenal :
f(x) = 2x + 5
g(x) = 3x – 7
Menjawab:
(kabut)(x) = f (g(x))
= 2g(x) + 5
= 2(3x – 7) + 5
= 6x – 14 + 5
= 6x – 9
Hasil dari (kabut)(x) adalah 6x – 9
Contoh Soal 2
Diketahui fungsi f(x) = 4x + 3 dan juga fungsi g(x) = x-1. Pertanyaannya adalah (gof)(x) = (kabut)(x)?
Menjawab:
Dari sifat-sifat fungsi yang telah dipelajari sebelumnya yaitu fungsi komposisi tidak selalu komutatif. Oleh karena itu, cobalah mengujinya dengan persamaan yang ada.
Dikenal:
f(x) = 4x + 3
g(x) = x-1
(gof)(x) = (kabut)(x)
g(f(x)) = f(g(x))
g(4x + 3) = f(x-1)
4x + 3 -1 = 4(x-1) + 3
4x +2 = 4x – 4 + 3
4x + 2 ≠ 4x – 1
Dari hasil tersebut, ternyata teori sifat komutatif dapat dibuktikan dengan benar. Bahwa fungsi g dan x ketika disusun tidak akan menghasilkan hasil yang sama.
Contoh Soal 3
Diketahui f(x) = √(x+1) dan (fog)(x) = 2 √(x-1). Oleh karena itu tentukan nilai g(x)
Menjawab:
Dikenal
f(x) = x+1
(kabut)(x) = 2 √(x-1)
f (g(x) = 2 √(x-1)
√(g(x) + 1) = 2 √(x-1) artinya setiap sisi dipangkatkan menjadi 2
g(x) + 1 = 4(x – 1)
g(x) = 4x – 4 – 1
g(x) = 4x – 5
Jadi nilai g(x) adalah 4x – 5
Contoh Soal 4
Diketahui fungsi f(x) = 6x – 3 dan fungsi g(x) = 5x + 4 sedangkan (fog)(a) = 81. Maka tentukan nilai a
Menjawab:
Dikenal :
f(x) = 6x – 3
g(x) = 5x + 4
(kabut)(a) = 81
Jawab, maka nilai a adalah
f(g(a)) = 81
f(5a + 4) – 3 = 81
30a + 24 – 3 = 81
30a + 21 = 81
30a = 60
a = 2
maka nilai a adalah 2
Menghitung fungsi komposisi sebenarnya bisa dibalik, tergantung variabel mana yang diketahui. Sedangkan yang terpenting tidak bertentangan dengan sifat komposisinya. Anda dapat menggunakan berbagai cara untuk menemukan nilai yang tidak diketahui.
Itulah beberapa kesamaan fungsi komposisi. Anda bisa mempelajarinya lebih banyak untuk bisa mendapatkan lebih banyak pengetahuan tentangnya. Sehingga nantinya lebih mudah dalam menjawab berbagai pertanyaan yang diberikan.
Baca Juga Artikel Lainnya :
- Fungsi caliper, cara pakai, contoh soal dll
- Contoh Limit Fungsi Aljabar dan Jawabannya
- Bilangan dengan Pangkat Pecahan, Bentuk Akar, dan Contoh Soal
- Kuantitas Turunan Bersama Satuan, Dimensi, dan Contoh
- Pola Bilangan Segitiga, Fibonacci, Ganjil, Kotak, Dll (Lengkap)
- Ciri-Ciri Pangkat Beserta Pengertian, Sifat & Contoh Soal